- 积分
- 9841
- 回帖
- 0
- 西莫币
-
- 贡献
-
- 威望
-
- 存款
-
- 阅读权限
- 120
- 最后登录
- 1970-1-1
该用户从未签到
|
楼主 |
发表于 2020-8-2 17:48
|
显示全部楼层
来自: 中国山东济南
第三步:看!它左手右手一个慢动作!
我们已经知道如何用 MATLAB 搭建一个简单的机器人了。然而这样搭建的机器人,和小朋友用积木搭建的玩具并无二致 —— 既然是用软件做成的机器人,我们自然希望它能动起来。我们以加拿大机器人公司 Kinova 的第三代机械臂为例,来看看 MATLAB 如何让这支麒麟臂动起来。

在 MATLAB 界面中输入
>> robot = loadrobot("kinovaGen3");
>> showdetails(robot)
我们可以看到输出如下

不难看出,第三代 Kinova 是由 8 根连杆和 8 个关节拼接而成。如果我们要想知道某个具体连杆的信息,例如名叫 “Shoulder_Link” 的连杆, 依次输入
>> robot.getBody( Shoulder_Link ).Joint
>> robot.getBody( Shoulder_Link ).Joint.JointToParentTransform
>> robot.getBody( Shoulder_Link ).Joint.ChildToJointTransform
即可分别查询属于该连杆的关节,以及关节到母连杆和子连杆的转移矩阵。如此一来,我们就可以从这种方法重建出第三代 Kinova 机械臂了!
现在我们有两种方法可以让让机械臂动起来。第一种方法是通过变换关节旋转角度的方式,这种方法叫正运动学(Forward kinematics);第二种方法是通过给定每个连杆末端位置,这种方法叫逆运动学(Inverse kinematics)。正运动学可以很方便地对机械臂进行直接操控,而逆运动学则更有利于直接指定机械臂完成任务,例如抓取处于某位置的快递等等。这两种方法各有千秋。
有几何背景的读者知道,n 维欧式空间中的刚体形变可分为平移(Translation)、旋转(Rotation)和镜像(Reflection)三种,这三种变化可以用群作用,或者矩阵来表示。由这三种作用组成的群叫做欧几里得群(Euclidean Group)记作 E(n),因为 E(n) 中的元素都可以用矩阵表示,所以 E(n) n+1 阶矩阵群的子群(具体解释见下图)。群 E(n) 中只由平移和旋转(不含镜像)构成的子群叫做特殊欧几里得群,记作 SE(n)。

下面我们 MATLAB 中的逆运动学函数 inverseKinematics 来让机械臂动起来。我们只需要定义出机械臂所要经过的几个路径点的位置、速度以及加速度,MATLAB 即可通过对特殊欧几里得群求逆来计算出整个机械臂所经过的路径,以及每个时刻的速度以及加速度等信息。
% 关节起始旋转角及初始位置
positions = [2*pi, 0.2619, pi, 4.0142, 2*pi, 0.9598, pi/2];
config = homeConfiguration(robot);
for k = 1:length(positions)
config(k).JointPosition = positions(k);
end
% 定义机械臂需要通过的路径点以及对应速度、加速度信息
waypoints = [0.5639 0.0013 0.4336] + [-0.1 0.2 0.4 ; -0.2 0 0.1 ; -0.1 -0.2 0.4 ;] ;
waypointTimes = 0:4:8;
ts = 0.2;
trajTimes = 0:ts:waypointTimes(end);
waypointVels = 0.1 *[ 0 1 0; -1 0 0; 0 -1 0;] ;
waypointAccels = zeros(size(waypointVels));
waypointAccelTimes = diff(waypointTimes)/4;
[q,qd,qdd] = trapveltraj(waypoints,numel(trajTimes), ...
AccelTime ,repmat(waypointAccelTimes,[3 1]), ...
EndTime ,repmat(diff(waypointTimes),[3 1]));
% 画出初始状态
%% 画图--机械臂
show(gen3,config, Frames , off , PreservePlot ,false);
hold on
%% 画图--路径初始化
hTraj = plot3(waypoints(1,1),waypoints(2,1),waypoints(3,1), b.- );
set(hTraj, xdata , q(1,:), ydata , q(2,:), zdata , q(3,:));
%% 画图--路径点
plot3(waypoints(1,:),waypoints(2,:),waypoints(3,:), ro , LineWidth ,2);
set(gca, Position , [-.2, -.2, 1.5, 1.5]);
xlim([-1 1]), ylim([-1 1]), zlim([0 1.2]);
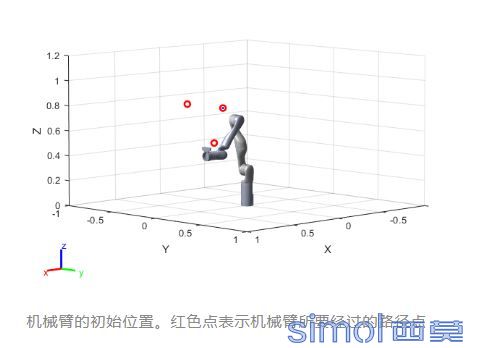
% 初始化机械臂的逆运动学方程
ik = inverseKinematics( RigidBodyTree ,robot);
ikWeights = [1 1 1 1 1 1];
ikInitGuess = robot.homeConfiguration; % 随机设置一个初始状态
% 让机器人动起来!
for idx = 1:numel(trajTimes)
% 解逆运动学方程
tgtPose = trvec2tform(q(:,idx) );
[config,info] = ik( EndEffector_Link , tgtPose,ikWeights,ikInitGuess);
ikInitGuess = config; % 以上一时刻的状态作为下一时刻的初始值
% 画出机器人的动态
show(robot,config, Frames , off , PreservePlot ,false);
title([ Trajectory at t = num2str(trajTimes(idx))])
drawnow
end
最后得到的轨迹图如下:
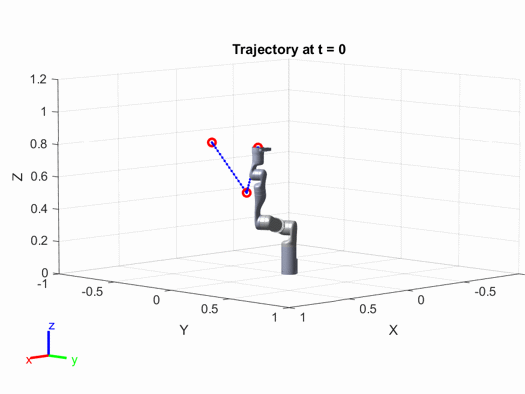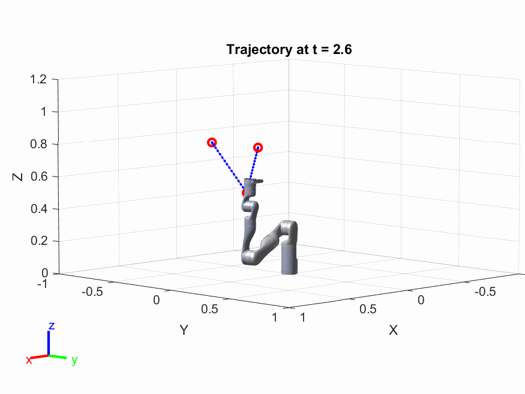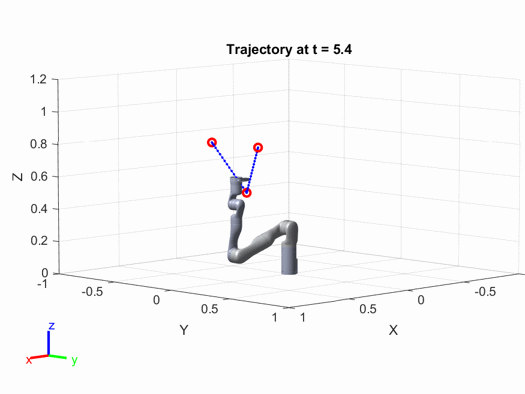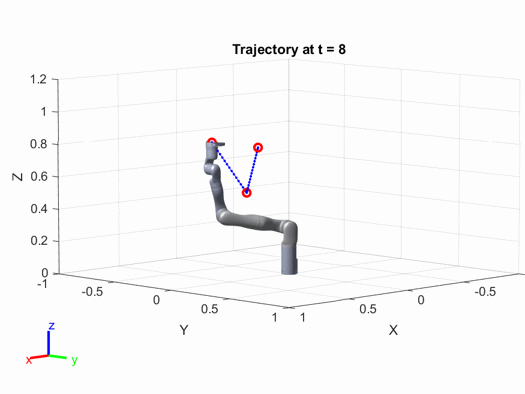
有兴趣的读者可以修改上面代码中的参数(例如路径点的位置、机械臂的速度加速度等),来看看结果会出现怎样的变化。
|
|

 加群请注明论坛用户名及所从事专业,否则不予通过
加群请注明论坛用户名及所从事专业,否则不予通过
 加群请注明论坛用户名及所从事专业,否则不予通过
加群请注明论坛用户名及所从事专业,否则不予通过
 加群请注明论坛用户名及所从事专业,否则不予通过
加群请注明论坛用户名及所从事专业,否则不予通过
 加群请注明论坛用户名及所从事专业,否则不予通过
加群请注明论坛用户名及所从事专业,否则不予通过
 加群请注明论坛用户名及所从事专业,否则不予通过
加群请注明论坛用户名及所从事专业,否则不予通过
 加群请注明论坛用户名及所从事专业,否则不予通过
加群请注明论坛用户名及所从事专业,否则不予通过
 |Archiver|手机版|小黑屋|西莫电机圈
( 浙ICP备10025899号-3|
|Archiver|手机版|小黑屋|西莫电机圈
( 浙ICP备10025899号-3|![]() 浙公网安备33010502012192号 )
浙公网安备33010502012192号 )