马上注册，结交更多好友，享用更多功能，让你轻松玩转社区。
您需要 登录 才可以下载或查看，没有账号？立即注册
×
同步电机的电抗参数及基于磁场仿真的数值计算
1. 引言
参数计算是电机电磁设计的核心，电机最终的各性能主要取决于绕组的各项参数。电机的参数包括绕组的电阻参数和电抗参数，电阻参数主要取决于构成电路的材料和结构特性，由于电路的材料和结构比较简单，且材料的导电特性通常是线性的，电路结构也是固定的，因此电阻参数较为容易计算。电抗参数则不然，它既与电路的特性有关也与磁路的特性有关，而电机中随着转子的旋转，磁路结构也在不断地变化，更令人头疼的是磁路结构复杂，构成磁路的材料有多种，有齿槽影响，有气隙的影响，铁芯的导磁特性为非线性等等，这使得电抗参数的准确计算变得极其复杂，通常的基于路的计算方法精度不够，而基于场的仿真计算方法又过于复杂，物理意义不够直观，难以理解。经常遇到电磁设计工程师咨询电抗参数的有关问题，西莫论坛上询问电抗参数问题的帖子比比皆是。从提问的情况看，主要包括：对电抗参数的概念不清；各种电抗参数的物理意义及理解不到位；电抗参数的计算方法及测定方法；各种电抗参数对电机各项性能的影响等。针对以上问题，本文从基本物理概念出发，为大家梳理一下有关绕组电抗参数的概念，在此基础上提出基于磁场仿真的简易数值计算方法，篇幅所限，不可能面面俱到，有关电抗参数的测试及与电机性能的关系，本文不做详细阐述，或仅就本文遇到的有关内容进行必要的阐述。 2. 电抗参数的概念2.1 线圈自感和互感
众所周知，电机是以磁场为介质，基于电磁感应等一系列电磁定律来实现机电能量转换的装置，这就决定了电机的构成离不开线圈，而正是由于各种线圈的存在，才能在电机中建立磁场以及磁场与通电导体的相互作用。线圈即电感，线圈的电感与通电角频率的乘积即为线圈的电抗。因此电抗参数的计算实质上是线圈各种电感的计算。 2.1.1 自感
单个线圈通以电流会产生磁场（磁通），如图1所示，我们将单个线圈通电后产生磁通的能力称为该线圈的自感。定义：线圈通以单位电流（即1A电流）产生的匝链线圈本身的磁通是为该线圈的自感值L，即： L=Φ/I 式中：I为线圈中所通的直流电流（A），Φ为通电后线圈产生的磁通（Wb），L为自感（H）。 (a)空心线圈 (b)有铁芯的线圈 图1 线圈的自感 从自感的定义可知，所谓自感也就是一只线圈通1A电流时所产生的磁通量。显然，同样匝数的线圈通同样大小的电流所产生的磁通多少与线圈的磁路有密切关系，如果把线圈绕在铁芯上，由于铁芯的磁导率远高于空气，所以产生的磁通的能力要强许多倍。理论研究表明，线圈的自感与线圈的匝数及磁路的磁导有关，其关系式为L=N2Λ，式中：N为线圈匝数，Λ为磁路的磁导，磁导的大小与磁路的长度、磁路截面积以及磁路材料的磁导率等参数有关，即： Λ=μ·S/l 式中μ为磁路材料的磁导率，S为磁路的截面积，l为磁路长度。 2.1.2 互感
当多个线圈共用一个磁路时，除了每个线圈存在自感以外，任何一个线圈通以电流时，所产生的磁通还匝链其他线圈，在其他线圈中产生感应电势，这就提出了一个互感的问题，如图2所示，所谓互感，就是在一个线圈A中通以单位电流时，产生的匝链于线圈B的磁通，即称为线圈AB之间的互感，由于两线圈所处的相对位置是相对固定的，所以两线圈的互感是可逆的，即： Lab=Lba= Φab/Ia=Φba/Ib=M 互感的大小除了与两个线圈的匝数有关，还与两线圈的相对位置及共用磁路的磁导有关。 图2 线圈的互感 2.2 电机绕组的电感
2.2.1 转子均匀时绕组的电感
我们以交流电机为例，讲一讲电机绕组的电感，如图3所示，交流电机的电枢上布有三相对称绕组，其匝数相同，三相绕组轴线互差120°空间电角度，当转子是一个各向对称的均匀转子时，如异步电机转子和隐极同步电机转子，各相绕组的磁路磁导与转子位置无关，且各相绕组之间的相对位置和互感磁路磁导也不变，因此忽略铁芯饱和的情况下，各相绕组的自感和互感均为常数，即 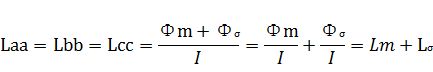互感为 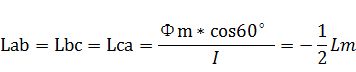图3 电机绕组的电感 2.2.2 非对称转子时绕组的电感
当转子各向磁导不对称时，如凸极同步电机或永磁电机转子，由于绕组磁路的磁导与转子位置有关，所以各相绕组的自感和互感就成为了转子位置的函数，如图4所示。 图4 凸极同步电机的电感 由图4可见，当转子直轴正对A相绕组轴线时，A相绕组自感最大为Laad，同时BC相绕组的互感绝对值最小，实际值为负值；转子交轴对齐A相绕组轴线时，A相绕组自感最小为Laaq，同时BC相绕组互感的绝对值最大。随着转子位置的不同，自感和互感分别以恒值Ls0和Ms0为中心呈二倍频余弦波动，各相绕组的自感和互感为： 式中： Ls0=Lσ+(Laad+Laaq)/2，Ls2=(Laad-Laaq)/2，Ms0=Mσ+(Laad+Laaq)/4，Ms2=(Laad-Laaq)/2。Lσ和Mσ分别为漏自感和漏互感。Laad和Laaq分别为直轴和交轴对齐某相轴线时，该相绕组的电枢反应电感。 2.2.3 直轴和交轴电感
以上讨论的是在定子abc坐标系下各相绕组的自感和他们之间的互感，其物理意义较为直观，各电感值就是实际绕组的电感值。对于异步电机这样的各向均匀对称的转子，各相绕组的自感及互感均为常数，因此异步机可以得到一个以绕组恒定参数组成的等效电路。但对于同步电机而言，其绕组电感参数与转子位置有关，是转子位置的函数，当转子旋转时也就是时间的函数，虽然这些参数都是实际绕组的物理实际值，但由于参数随时间变化，使得分析电机的性能及各种方程式十分繁杂，为了简化同步电机的分析、计算，我们希望得到恒定的电抗参数，为此分析同步电机时，通常采用转子dq轴坐标系。在dq坐标系下，电抗参数变成了恒定值，电流电压也变成了直流值，这就是通常说的Park坐标变换，由abc坐标变换到dq坐标的电感，数学推导过程繁杂，这里只给出结果，详细推导参见相关教科书。
Ld=Lσ + Mσ +3Laad/2= Lσ +Mσ + Lad Lq=Lσ + Mσ +3Laaq/2= Lσ +Mσ + Laq 经过以上变换，绕组的电感参数大为简化，由原来的时变量变为了恒定量，但其物理意义被弱化了，为了便于后续仿真计算的理解，我们详细阐述一下，交直轴电抗的物理意义。我们知道，三相对称绕组通以三相对称交流电时便在气隙中产生旋转磁场。设想在定子上设置两个空间互差90°电角度，匝数节距与一相交流绕组完全相同的绕组，分别给他们通以直流电流同样会在气隙中产生一个固定的磁场，调节两个绕组的电流大小和方向可以改变该固定磁场的大小和空间位置，我们完全可以通过调节两个绕组的电流，使其产生的合成磁场与三相交流绕组通以三相交流电在某一时刻所产生的合成磁场大小相等，位置重合，然后再将两个虚拟绕组同时以转子速度旋转，这样两个直流绕组产生的磁场就和三相交流绕组所产生的旋转磁场完全等效。因此我们就完全可以用这两个旋转的直流绕组去替代三相交流绕组，我们可以把其中一个直流绕组的轴线设置在与转子d轴对齐位置，称为d轴绕组，另一个直流绕组轴线与转子q轴对齐称为q轴绕组，两个绕组始终与转子同步旋转，这样交直轴绕组的磁路就相对固定，所反映的电感值也不会随时间变换了，而且由于dq轴绕组相互垂直，不存在互感，这就大大简化了绕组的参数和同步电机的分析计算。综上所述，上式反映的电感参数其实就是当转子d轴对齐某相绕组轴线时，该相绕组的电感值即为Ld，当转子q轴对齐某相绕组轴线时，该相绕组的电感值即为Lq，当然考虑到原来三相绕组之间存在互感，一相绕组通电时，另外两相中的电流也会对该相绕组产生互感磁通，因此需要把一相绕组的主电感（电枢反应电感Laad）放大3/2倍才能达到完全等效，这就是上式的物理意义。
在电励磁同步电机中，转子直轴上会布置有励磁绕组，交直轴上还都布置有阻尼绕组，这些绕组都会与定子绕组存在互感。由电机学知识可知，如果把励磁绕组和阻尼绕组都看作超导体绕组，那么这些超导绕组会产生阻止磁通穿越它的作用，这样交直轴绕组产生的磁通会被迫排挤到漏磁路中，磁导急剧减小，此时交直轴绕组所反映出的电感就会比稳态时的Ld、Lq小许多，我们分别称之为交直轴超瞬变电感，记为Ld″和Lq″；若只有直轴励磁绕组为超导，阻尼绕组开路，可见磁通穿越了阻尼绕组却无法穿越励磁绕组，这样直轴电感会小于稳态电感Ld但大于超瞬变电感Ld″，我们称之为瞬变电感记为Ld′，由于交轴无励磁绕组，故不存在交轴瞬变电感问题。 3. 同步电机电抗的仿真计算了解了同步电机交直轴电感的物理意义，我们就可以从各电抗的定义出发用电磁场有限元软件进行各种交直轴电感的仿真计算，本文介绍的这种计算方法较传统的瞬态场计算更加简便易行，精度更高，计算时间更短，占用计算机资源更少。由于现代计算软件的材料属性可以任意编辑设置，使得该方法较实测还要方便直观，更加简便易行可操作。 3.1 交直轴电抗Xd、Xq的计算方法
计算步骤如下： A、瞬态场，按实际电机尺寸建立几何模型。 B、使转子d轴与A相轴线对齐， Ansoft一键有限元生成的模型默认的转子初始位置即为d轴与A相轴线对齐，此时只给A相通电产生的磁场如下。 图5 A相通电产生的d轴磁场 C、设置转子励磁绕组和阻尼绕组的电阻为无穷大（即二者均开路）；永磁电机设置永磁体为空气，设置电枢绕组电阻为0。 D、转速设置为0，使转子保持静止，按下图任一方式施加电流激励。如果A相绕组与转子d轴对齐，按照图a加电流激励，则三相电流激励可以为 Ia=Im cos（wt），Ib= -0.5 Im cos（wt），Ic= -0.5 Im cos（wt）。
图6 施加激励 E、 仿真计算出电压有效值U。 F、结果处理，若按a）图施加激励则Xd=U/I，I为电流有效值，若按图b）施加单相激励，则Xd=3U/2I。需要指出的是单相激励时由于后处理也将漏抗同时放大了3/2倍，会引起一定的误差，但由于漏抗远小于主电抗，因此误差不大，工程上精度足够。如果精确计算需要先将漏抗与主电抗分离，详细方法不在赘述，推荐图a）施加混联激励。 对于交轴电抗与上述步骤相同，只是B步骤变为将转子交轴与A相绕组轴线对齐即可，其余步骤不变。 3.2 瞬变电抗的仿真计算
步骤与3.1相同，只是C步骤变为：设置转子励磁绕组和阻尼绕组电阻为0，即超导体短路。具体软件操作是将二者材料的电阻率改为非常大，例如1e12；同时需要将励磁绕组改为solid；并且使励磁绕组短路，可以使用电压激励，同时电压设置为0。 另外为了使电枢反应磁场经转子漏磁路闭合，实际仿真时还需要将定子电流初始值设置0，然后再施加三相电流源。可通过if函数实现，例如，A相电流源表达式为if（time<0.001s,0A, Im*cos（ωt）），其他两相可仿此赋相应电流。此处注意，为了计算时，使求解结果容易收敛，电流激励的频率不宜过大，工频即可。其余步骤不变，得到的电抗即为交直轴超同步电抗Xq″、Xd″，图7为励磁绕组和阻尼绕组为超导体时磁力线分布情况，由图7可见磁通未穿越励磁绕组和阻尼绕组，被挤到漏磁路上，因此Xq″、Xd″很小。 图7 励磁绕组和阻尼绕组为超导体时磁力线分布情况 若设置阻尼绕组开路，即将阻尼绕组材料设置为电导率非常小的材料例如2，励磁绕组依然为超导体短路，则得到直轴瞬变电抗Xd′。图8为此时的磁力线分布，可见磁通只穿越了阻尼绕组，但未穿越励磁绕组。 图8 阻尼绕组开路励磁绕组超导体短路磁力线分布情况 4. 结束语本文介绍了同步电机各种电抗参数的定义和物理意义，在此基础上，从各种电抗的定义出发提出了各种电抗参数的电磁场仿真计算方法，由于现代仿真计算软件可以灵活设置激励和材料属性，使得该方法非常简便易行，大大减小了计算工作量和计算时间，精度较高，比实物测试更加直观简单。
| 
加群请注明论坛用户名及所从事专业，否则不予通过
|Archiver|手机版|小黑屋|西莫电机圈
( 浙ICP备10025899号-3|
浙公网安备：33028202000436号 ) 
IP卡
发表于 2018-3-30 21:51
提升卡
置顶卡
喧嚣卡
变色卡
显身卡
发表于 2018-3-30 21:59
发表于 2018-3-31 10:15
但是楼主插入的图片好像无法显示啊，难道是我这里的问题嘛。楼主能发个文档或者告诉书名吗 谢谢